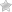Solving a Quadratic Equation Using the AC-Method

Solve the following quadratic equation using the AC-method:
\[
7x^2 – 2x – 5 = 0
\]

Solution
Step 1: Identify the values of \(a\), \(b\), and \(c\)
The quadratic equation is in the form \(ax^2 + bx + c = 0\), where:

• \(a=7\)
• \(b=−2\)
• \(c=−5\)

Step 2: Multiply a and c
Now, multiply the coefficients \(a\) and \(c\):

\[
a \times c = 7 \times (-5) = -35
\]
Step 3: Find two numbers that multiply to \(a.c\) and add to $\backslash (b\backslash )$
We need to find two numbers that multiply to $-\backslash (35\backslash )$
\[
a \times c = 7 \times (-5) = -35
\]
And add to $-\backslash (2\backslash )$ (the coefficient $\backslash (b\backslash )$).

The two numbers that satisfy this condition are $\backslash (5\backslash )$ and $\backslash (7\backslash )$ because:
\[
a \times c = 7 \times (-5) = -35
\]
and
\[
5 + (-7) = -2
\]
Step 4: Rewrite the middle term
Now, rewrite the middle term, \( -2x \), using the two numbers we found, \( 5x \) and \( -7x \):

\[
7x^2 – 7x + 5x – 5 = 0
\]
Step 5: Factor by grouping
Group the terms in pairs:

\[
(7x^2 – 7x) + (5x – 5) = 0
\]

Now, factor out the greatest common factor (GCF) from each group:

\[
7x(x – 1) + 5(x – 1) = 0
\]
Step 6: Factor out the common binomial factor
Both terms contain the binomial \((x – 1)\), so factor it out:

\[
(x – 1)(7x + 5) = 0
\]
Step 7: Solve for \(x\)
Set each factor equal to zero and solve for \(x\):

\[
x – 1 = 0 \quad \Rightarrow \quad x = 1
\]

\[
7x + 5 = 0 \quad \Rightarrow \quad 7x = -5\]

(No Ratings Yet)

Loading...