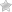Given the following system of linear equations, solve for \(x\) and \(y\):
\[
\left\{
\begin{array}{l}
5x + 3y = -4 \\
x – 3y = 10
\end{array}
\right.
\]
Solution
We can solve this system using substitution or elimination. Here, we will use the substitution method.
Step 1: Solve one equation for one variable
Let’s solve the second equation for \( x \):
\[
x – 3y = 10
\]
Add \( 3y \) to both sides:
\[
x = 10 + 3y
\]
Now we have \( x \) in terms of \( y \).
Step 2: Substitute this expression for \( x \) into the first equation
Substitute \( x = 10 + 3y \) into the first equation:
\[
5(10 + 3y) + 3y = -4
\]
Step 3: Simplify and solve for \( y \)
Expand the equation:
\[
50 + 15y + 3y = -4
\]
Combine like terms:
\[
50 + 18y = -4
\]
Subtract 50 from both sides:
\[
18y = -4 – 50 \quad \Rightarrow \quad 18y = -54
\]
Divide both sides by 18:
\[
y = \frac{-54}{18} \quad \Rightarrow \quad y = -3
\]
Step 4: Substitute \( y = -3 \) back into the equation for \( x \)
Now substitute \( y = -3 \) into the equation
\[
x = 10 + 3y \quad \Rightarrow \quad x = 10 + 3(-3) \quad \Rightarrow \quad x = 1
\]
Step 5: Final solution
The solution to the system of equations is:
x = 1, \, y = -3
\]
This is the point where the two lines intersect: \( (1, -3) \).
(No Ratings Yet)
Loading...