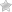Solve for \(x\) where
\[
-4|6x + 2| = -16
\]
Solution
To solve the absolute value equation \(-4|6x + 2| = -16\), follow these steps:
Step 1: Divide both sides by \(-4\)
We start by isolating the absolute value expression. Divide both sides of the equation by \(-4\):
\[
|6x + 2| = 4
\]
Step 2: Set up two cases for the absolute value
Since the absolute value of an expression is equal to 4, we can set up two possible cases:
-
\[
6x + 2 = 4
\] -
\[
6x + 2 = -4
\]
Step 3: Solve each case
Case 1: \(6x + 2 = 4\)
Subtract 2 from both sides:
\[
6x = 4 – 2
\]
\[
6x = 2
\]
Now divide both sides by 6:
\[
x = \frac{2}{6} = \frac{1}{3}
\]
Case 2: \(6x + 2 = -4\)
Subtract 2 from both sides:
\[
6x = -4 – 2
\]
\[
6x = -6
\]
Now divide both sides by 6:
\[
x = \frac{-6}{6} = -1
\]
Step 4: Final solution
The two possible solutions are:
x = \frac{1}{3} \quad \text{or} \quad x = -1
\]